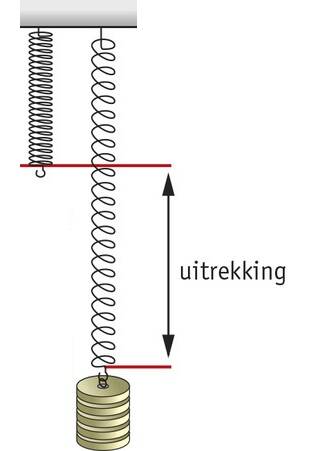
Veerkracht
Wanneer je een veer probeert uit te rekken merk je dat hoe verder je hem uitrekt, hoe meer kracht je daarvoor moet leveren. Dit volgt uit de wet van Hooke: de veerkracht die een veer levert is rechtevenredig met de uitrekking of indrukking van die veer. Dit betekent dat als je de veer 2 keer zo ver uitrekt (of indrukt, bij een drukveer) de veerkracht 2 keer zo groot wordt. De kracht die jij moet leveren om de veer uitgerekt te houden is even groot als de veerkracht, dit volgt uit de eerste wet van Newton.
Veerconstante
Er zijn heel veel verschillende soorten veren: trekveren (die je uit kunt rekken) en drukveren (die je in kunt drukken), hele grote en hele kleine veren, hele sterke en hele slappe veren. Iedere veer heeft zijn eigen veerconstante. De veerconstante C geeft aan hoeveel kracht er nodig is om de veer één meter uit te rekken. De eenheid van de veerconstante is dan ook newton per meter (N/m). Hij wordt echter ook vaak in newton per centimeter (N/cm) gegeven, in dat geval is er aangegeven welke kracht er nodig is om de veer één cm uit te rekken. Met behulp van de veerconstante kun je dus bij elke uitrekking berekenen hoe groot de veerkracht is, of andersom.
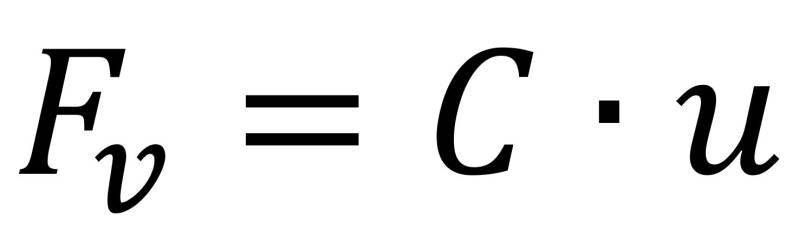
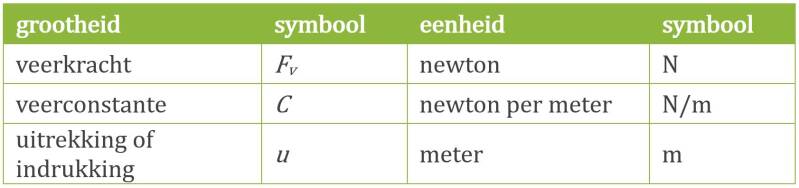
Aan de veerconstante kun je zien hoe sterk een veer is, immers een sterke veer levert een veel grotere veerkracht bij een uitrekking van één centimeter dan een slappe veer. Dus hoe hoger de veerconstante, hoe sterker (of: stugger) de veer is.
Massa aan een veer
Wanneer je een gewichtje aan een veer hangt zorgt de zwaartekracht op de massa voor de uitrekking van de veer. Als het gewichtje stil hangt geldt de eerste wet van Newton (als de snelheid van het voorwerp niet verandert is de resulterende kracht nul). De veerkracht is dan gelijk aan de zwaartekracht. Dit geldt natuurlijk ook wanneer je een massa op een drukveer legt: de zwaartekracht zorgt dan voor de indrukking van de veer.
[Hier komt een foto met veren met verschillende massa's er aan, en de zwaartekracht en veerkracht er in getekend.]
Massa's aan een veer. Wanneer de massa stil blijft hangen is de zwaartekracht gelijk aan de veerkracht. Daardoor is bij een grotere massa de uitrekking van de veer groter.
Rechtevenredig verband
Van elke veer kun je een grafiek maken waarin je de veerkracht uitzet tegen de uitrekking van de veer. De uitrekking is het verschil tussen de lengte van de veer als hij uitgerekt is en zijn lengte als er geen kracht op werkt. Als de veer voldoet aan de wet van Hooke is de grafiek een rechte lijn door de oorsprong: er is een rechtevenredig verband tussen de veerkracht en de uitrekking. Het hellingsgetal van de (veerkracht,uitrekking)-grafiek is dan gelijk aan de veerconstante van de veer.
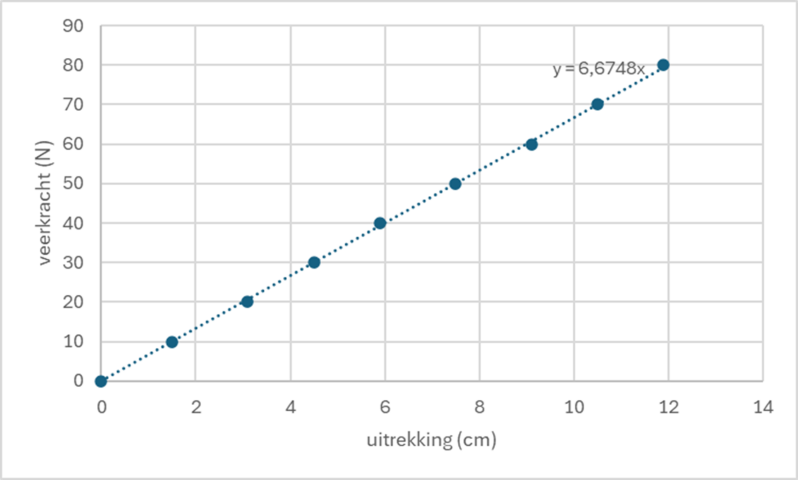
Deze veer voldoet aan de wet van Hooke: er is een rechtevenredig verband tussen de veerkracht en de uitrekking. Het hellingsgetal is de veerconstante, dus voor deze veer geldt C = 6,6748 N/cm.
Geen rechtevenredig verband
Er zijn heel veel voorwerpen of situaties waarin de veerkracht een rol speelt. Bekend zijn natuurlijk de veren die bijvoorbeeld in fitnessapparatuur, de trampoline, een matras of je balpen zitten. Maar ook bij bijvoorbeeld elastiekjes, een skippybal, stretch kleding of de doorbuiging van een houten tak is er sprake van een veerkracht. Het is lang niet altijd zo dat het (veerkracht,uitrekking)-diagram een rechte lijn is! Als er geen rechtevenredig verband is tussen de veerkracht en de uitrekking zeggen we dat de veer niet voldoet aan de wet van Hooke: het is geen ideale veer. Je kunt de formule van de veerkracht dan ook niet gebruiken.
Online lab: massa's en veren
Online lab: wet van Hooke
Bronvermelding afbeeldingen
Verschillende veren: Tudor Barker, Flickr - https://www.flickr.com/photos/tudedude/ - licentie CC BY-NC-SA 2.0
Trampolineveren: Veronica Faole, Flickr - https://www.flickr.com/photos/sleeplessnights/ - licentie CC BY-NC-ND 2.0
Vering auto: https://www.hulpveren.nl/
Fietszadel: macfred64, Flickr - https://www.flickr.com/photos/igel_rupert/ - licentie CC BY-NC 2.0
Man met veer: Ant, Flickr - https://www.flickr.com/people/ant-o-rama/ - licentie CC BY-NC-ND 2.0