Krachten tekenen en optellen

Een kracht is een voorbeeld van een vector: een grootheid waarvan niet alleen de grootte maar ook de richting van belang is. Een ander voorbeeld van een vector is de snelheid. Een kracht is niet zichtbaar, maar vaak is het wel fijn of nodig om een kracht te tekenen. Wanneer er meerdere krachten op een voorwerp werken wil je soms weten wat de totale kracht is. Maar bij vectoren werkt optellen een beetje anders dan je gewend bent, omdat de richting hier ook van belang is.

Een kracht tekenen

Vectoren teken je als een pijl. Daarbij zijn er vier dingen waar je op moet letten: het aangrijpingspunt, de richting, de grootte en de naam van de kracht. Nauwkeurig werken is hierbij altijd érg belangrijk!

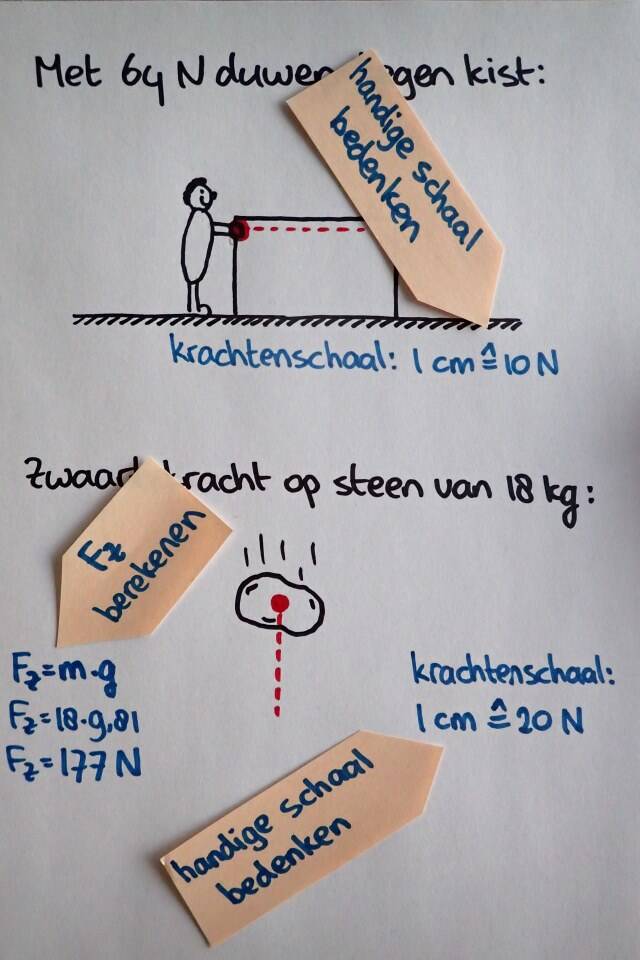
Twee voorbeelden van het tekenen van een kracht, stap voor stap.

Aangrijpingspunt van de kracht
Het aangrijpingspunt is de plek van het voorwerp waar de kracht precies wordt uitgeoefend. Als je met je handen tegen een kist aan duwt is het aangrijpingspunt van de duwkracht de plek waar je handen de kist raken. Wanneer een voorwerp aan een touwtje hangt is het aangrijpingspunt van de spankracht de plek waar het voorwerp aan het touwtje vast zit. Het aangrijpingspunt van de zwaartekracht is altijd het zwaartepunt. Zo kun je bij elke kracht bedenken wat het aangrijpingspunt is.

Richting van de kracht
Bij een vector is niet alleen de grootte maar ook de richting van belang. Daarom moet je de pijl die de kracht aangeeft altijd in de juiste richting tekenen. Bij de zwaartekracht is dat altijd naar beneden. Bij andere krachten zul je goed naar de situatie moeten kijken om de richting te bepalen.

Grootte van de kracht
De lengte van de pijl die je tekent geeft de grootte van de kracht weer. Hiervoor moet bij de tekening de krachtenschaal vermeld zijn. Een voorbeeld van de krachtenschaal is: 1 cm ≙ 20 N. Het symbool '≙' betekent 'komt overeen met'. Hier staat dus dat elke centimeter lengte van de pijl overeenkomt met een kracht van 20 N. Als de pijl bijvoorbeeld 4,2 cm lang is betekent dat een kracht van 4,2 x 20 = 84 N.

Naam van de kracht
Het is ook belangrijk dat je bij de getekende pijl zet dat het een kracht is en welke kracht. Meestal gebruik je hiervoor het symbool F met daaronder (in subscript) het nummer of de naam van de kracht.

Resulterende kracht

De 'totale kracht' die op een voorwerp werkt noemen we resulterende kracht, resultante of nettokracht. Omdat krachten vectoren zijn moet je bij het berekenen of bepalen van de resulterende kracht ook rekening houden met de richting van de krachten. Daarom kun je ze niet altijd gewoon optellen. In sommige situaties kun je de resulterende kracht berekenen, in andere situaties kun je de resulterende kracht bepalen met behulp van een tekening van de krachten op schaal.

Meerdere krachten in dezelfde of tegengestelde richting

Wanneer twee of meer krachten in dezelfde richting werken is de resulterende kracht de som van de uitgeoefende krachten. Je kunt de krachten dus gewoon bij elkaar optellen. Wanneer een kracht de andere kant op werkt, dus in tegengestelde richting, werkt die de andere kracht(en) tegen. Deze moet je er dan van af trekken om de resulterende kracht te berekenen.

Kop-staart-methode en parallellogrammethode

Het bepalen van de resulterende kracht kun je zien als het achter elkaar leggen van de verschillende vectorpijlen, we noemen dit de kop-staart-methode. Op deze manier kun je in alle situaties de resulterende kracht bepalen. Je hebt daarvoor een tekening nodig waarin de krachten op schaal staan weergegeven. Als je de resulterende kracht getekend hebt kun je met behulp van de krachtenschaal de grootte van de resultante bepalen.

Een andere manier om de resulterende kracht te bepalen is de parallellogrammethode. Ook hier heb je een tekening van de krachten met de krachtenschaal voor nodig. Je mag altijd zelf kiezen welke manier je gebruikt!

Twee krachten loodrecht op elkaar

Wanneer je de resulterende kracht gaat tekenen van twee krachten die loodrecht op elkaar staan ontstaat er een rechthoekige driehoek: een driehoek met een hoek van 90 graden er in. Voor zo'n driehoek geldt de wet van Pythagoras. Met behulp van die wet kunnen we dan dus de resulterende kracht berekenen!